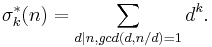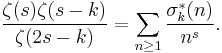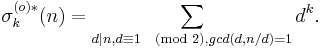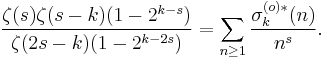Unitary divisor
In mathematics, a natural number a is a unitary divisor of a number b if a is a divisor of b and if a and 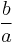 are coprime, having no common factor other than 1. Thus, 5 is a unitary divisor of 60, because 5 and
are coprime, having no common factor other than 1. Thus, 5 is a unitary divisor of 60, because 5 and 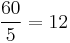 have only 1 as a common factor, while 6 is a divisor but not a unitary divisor of 60, as 6 and
have only 1 as a common factor, while 6 is a divisor but not a unitary divisor of 60, as 6 and 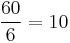 have a common factor other than 1, namely 2. 1 is a unitary divisor of every natural number.
have a common factor other than 1, namely 2. 1 is a unitary divisor of every natural number.
Equivalently, a given divisor a of b is a unitary divisor iff every prime factor of a has the same multiplicity in a as it has in b.
The sum of unitary divisors function is denoted by the lowercase Greek letter sigma thus: σ*(n). The sum of the k-th powers of the unitary divisors is denoted by σ*k(n):
If the proper unitary divisors of a given number add up to that number, then that number is called a unitary perfect number.
Contents |
Properties
The number of unitary divisors of a number n is 2k, where k is the number of distinct prime factors of n. The sum of the unitary divisors of n is odd if n is a power of 2 (including 1), and even otherwise.
Both the count and the sum of the unitary divisors of n are multiplicative functions of n that are not completely multiplicative. The Dirichlet generating function is
Odd unitary divisors
The sum of the k-th powers of the odd unitary divisors is
It is also multiplicative, with Dirichlet generating function
References
- Richard K. Guy (2004). Unsolved Problems in Number Theory. Springer-Verlag. p. 84. ISBN 0-387-20860-7. Section B3.
- Paulo Ribenboim (2000). My Numbers, My Friends: Popular Lectures on Number Theory. Springer-Verlag. p. 352. ISBN 0-387-98911-0.
- Cohen, Eckford (1959). "A class of residue systems (mod r) and related arithmetical functions. I. A generalization of Möbius inversion". Pacific J. Math. 9 (1): pp. 13—23. MR0109806.
- Cohen, Eckford (1960). "Arithmetical functions associated with the unitary divisors of an integer". Mathematische Zeitschrift 74: pp. 66—80. doi:10.1007/BF01180473. MR0112861.
- Cohen, Eckford (1960). "The number of unitary divisors of an integer". American mathematical monthly 67 (9): pp. 879—880. MR0122790.
- Cohen, Graeme L. (1990). "On an integers' infinitary divisors". Math. Comp. 54 (189): pp. 395—411. doi:10.1090/S0025-5718-1990-0993927-5. MR0993927.
- Cohen, Graeme L. (1993). "Arithmetic functions associated with infinitary divisors of an integer". Intl. J. Math. Math. Sci. 16 (2): pp. 373—383. doi:10.1155/S0161171293000456.
- Finch, Steven (2004). "Unitarism and Infinitarism". http://algo.inria.fr/csolve/try.pdf.
External links
- Weisstein, Eric W., "Unitary Divisor" from MathWorld.
- OEIS sequences: A034444 is σ0(n). A034448 is σ1(n). A034676 up to A034682 are σ2(n) to σ8(n).
A068068 is σ(o)*0(n). A192066 is σ(o)*1(n).
|
||||||||||||||||||||||